[No.42] MATLAB^®とC言語による開発の比較　- それぞれの言語を開発において有効活用する方法② -

2019.10.07

MBD

No.35にて、任意のカットオフ周波数をもつローパスフィルタの極を求める方法を説明しました。今回は、実際にMATLAB^®とC言語を用いて極の計算を行うプログラムを作成し、C言語と比較した場合のMATLAB^®の特長を解説します。

※No.35 [MATLAB^®とC言語による開発の比較　- それぞれの言語を開発において有効活用する方法① -] にて紹介した式で、今回の解説に使用する3点を下記に示します。
バタワースフィルタの振幅特性の理論式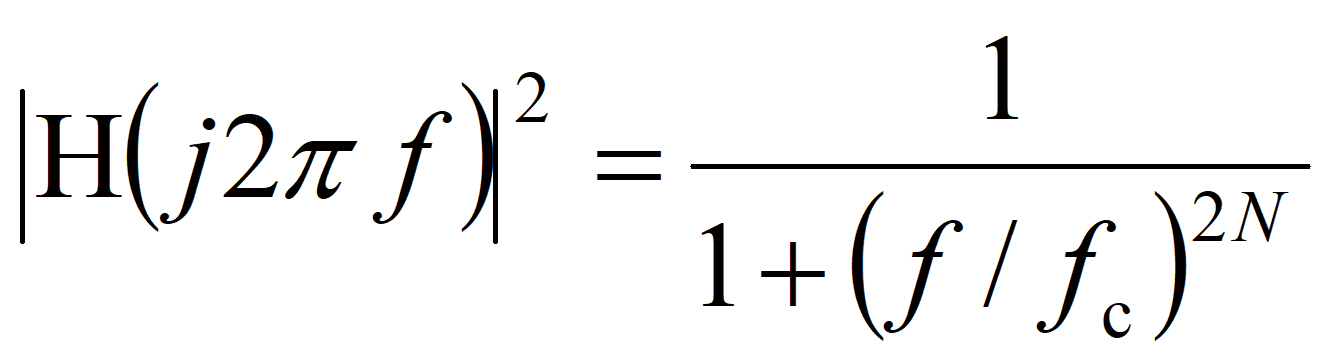：　　　（1）
オイラーの公式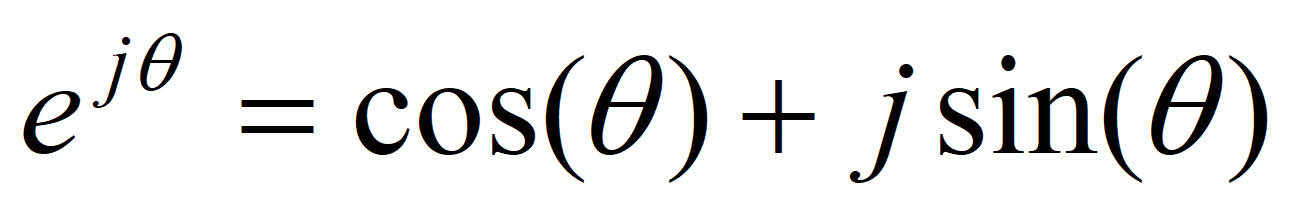：　　　（3）
カットオフ角周波数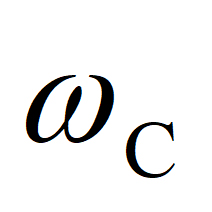に対する極の式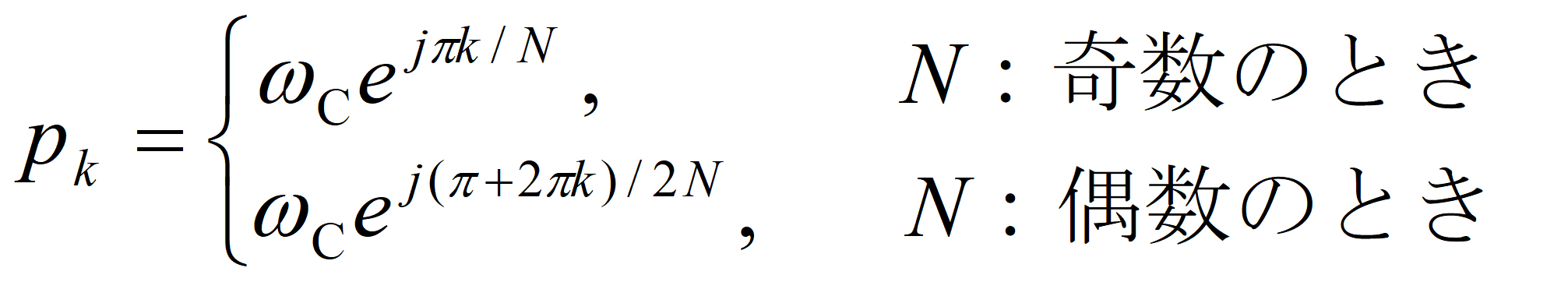：　　　（6）

2. MATLAB^®とC言語による開発の比較

2.2 極の導出

式（6）を用いてすべての極を計算して、その極の中から実部が負の極だけを抽出するMATLAB^®とC言語のプログラムをTable.1に示します。このプログラムでは、フィルタの次数を4、カットオフ角周波数を1と固定していますが、任意の値に変更することが可能です。

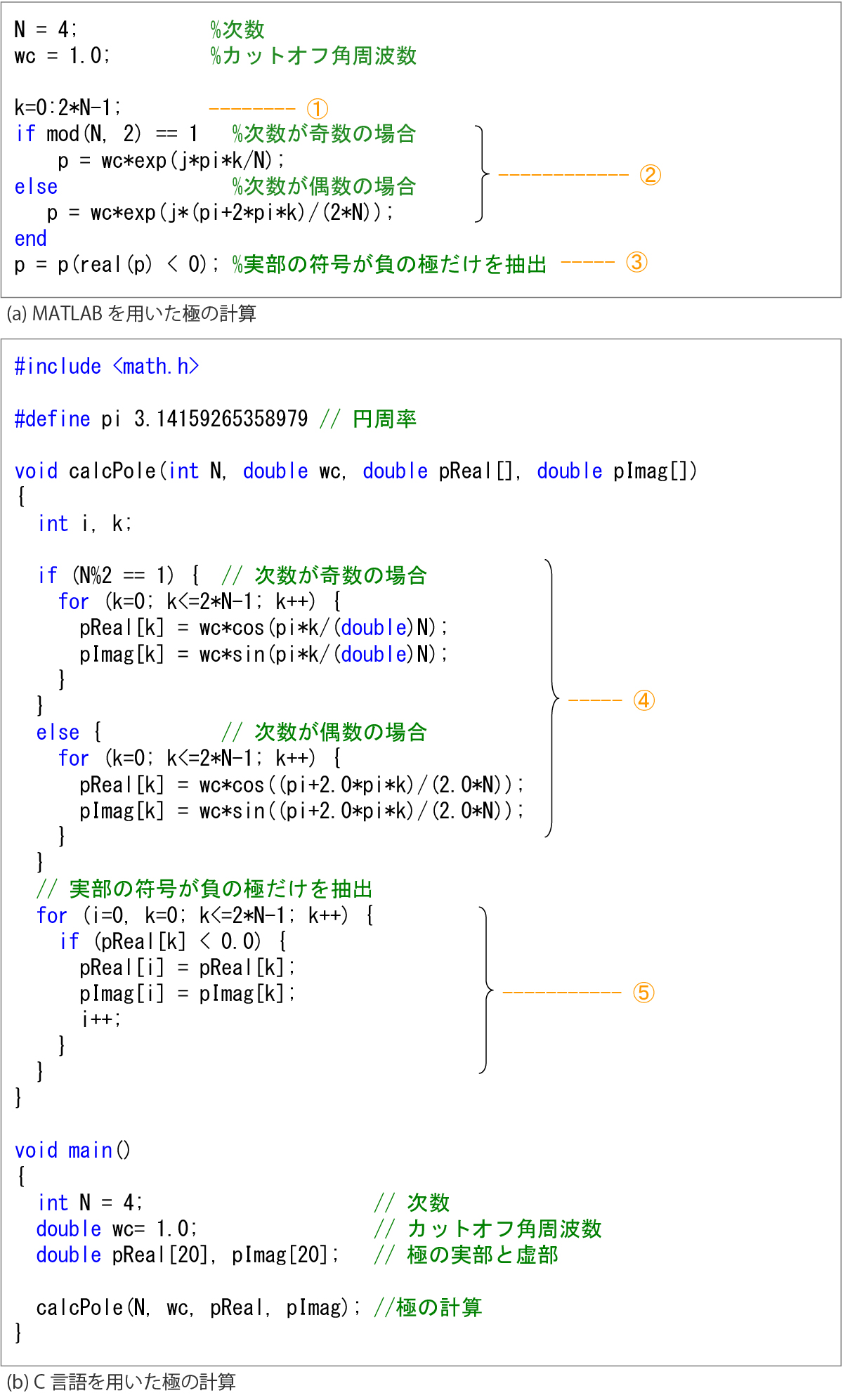Table.1　極を求めるプログラム

Table.1(a)のMATLAB^®のプログラムではが0からまで1ずつ増分する配列kを①に示されるコマンドで簡潔に記述することができ、さらに、この配列kを②に示されるように直接式の中に用いてベクトル計算を行うことができます。Table.1(b)のC言語の④の記述のようにfor文を用いて要素ごとに演算する必要がありません。また③はカッコ内の条件式が成立するとき、すなわち実部が負の場合の極の値をに代入するというコマンドで、C言語の⑤の記述をわずか1行で実現できます。

このようにMATLAB^®では配列に対してベクトル演算が定義されているため、非常に簡潔にプログラムを記述することができます。

また、式（6）に対応する②と④の記述を比較すると明らかなように、MATLAB^®では複素数演算をサポートしているため与えられた式に対して直感的にプログラムを記述することができます。一方、C言語では④のように式（3）を用いて極を実部と虚部に分けて計算する必要があります。この極を求めるプログラム全体では、MATLAB^®はC言語の約3分の1のコーディング量で済みます。

以上のことから、C言語と比較した場合のMATLAB^®の特長と効果は以下となります。

特長：

配列に対するベクトル演算をサポートしているのでプログラムを簡潔に記述できる
複素演算をサポートしているので理論式から直感的にプログラミングができる

効果：

簡潔に記述ができるのでバグの混入確率が低減する
理論式に対して直感的な記述ができるので開発効率が高い

2.3 伝達関数の導出

次に、個の極からバタワースフィルタの伝達関数を求めていきます。 No.35の2.2節、②の例のところで、フィルタの伝達関数の分母は極を用いた関数を掛け合わせたものになることを述べました。式で表すと下記となります。

　　（7）

この式は極が複素数なので、分母の式を展開するときに複素数の演算が必要になるためプログラムがかなり複雑になりそうですが、一工夫すると簡単に展開できます。複素数の極はFig.5に示されるようにそれぞれ共役なペアを持つので、これを利用すると実数の演算だけで式（7）を展開することができます。

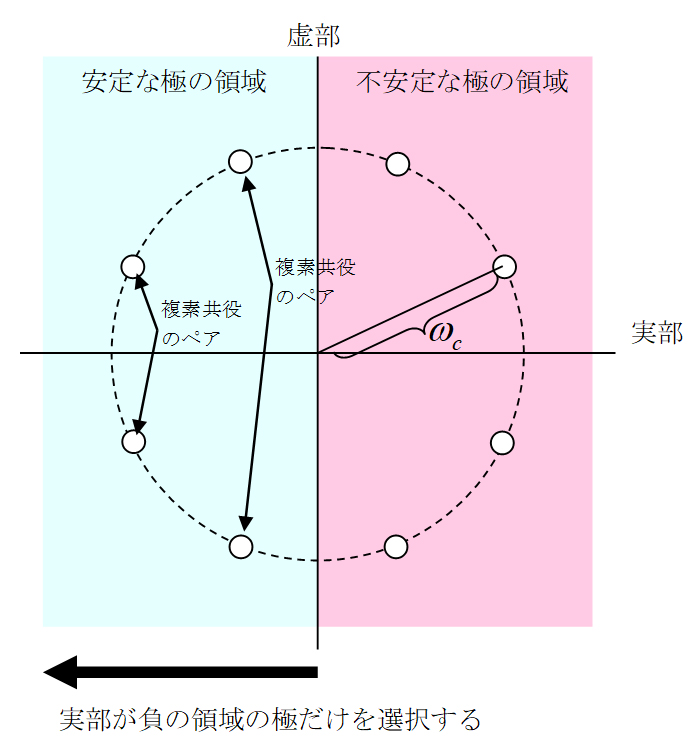Fig.5　極の選択方法

一つの極をのように実部と虚部に分けて表すと、その極と共役の関係にある極はと表すことができます。この2つのペアとなっている極の伝達関数は、次式の右辺のように実数だけの係数になります。

　　（8）

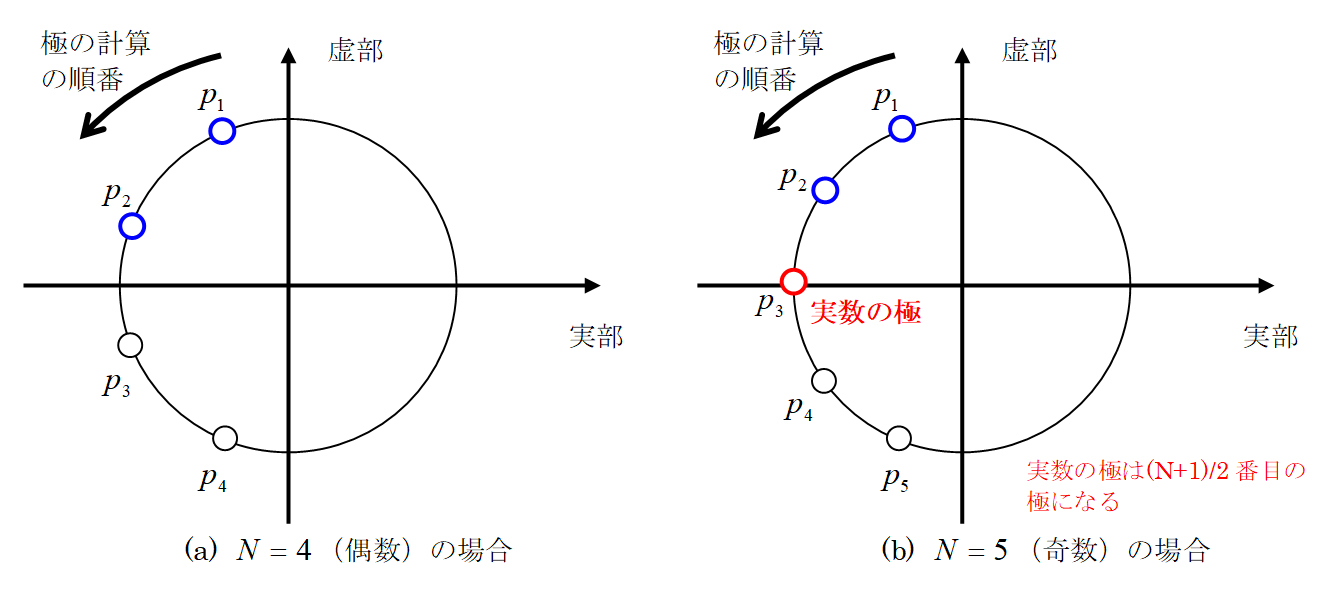Fig.6　フィルタの次数が偶数と奇数の場合の極の配置

Fig.6に示されるようにフィルタの次数が偶数の場合は、極が複素共役のペアだけとなるので、ペアの極に対する式（8）の伝達関数をそれぞれ掛け合わせることでフィルタの伝達関数が求まります。一方、フィルタの次数が奇数の場合は、1つの極（Fig. 6(b)の赤丸の極）だけが実数となるので、ペアの極に対する伝達関数と実数の極に対する伝達関数を掛け合わせることでフィルタの伝達関数が求まります。

掛け合わせた伝達関数を展開することで、フィルタの伝達関数は次式のようになります。

　　（9）

Table.1のプログラムでは、極はFig.6に示されるように単位円を反時計回りに順番に配列に格納されています。

以上のことを用いて、フィルタの伝達関数を求めるMATLAB^®とC言語プログラムをTable.2に示します。

Table.2(a)のMATLAB^®のプログラムでは、次数が奇数の場合は、①で実数の極に対する伝達関数の分母の係数を、aという係数の配列の初期値にしています。一方、偶数の場合は、aに1を初期値として与えています。そして②の部分で、この初期値とペアの極に対する伝達関数の分母をconv関数を用いて掛け合わせることで、式（9）の分母の係数を求めてaに代入しています。この多項式を掛け合わせるconv関数は、MATLAB^®では標準関数として提供されています。MATLAB^®では、このconv関数のような数学の汎用関数が数多く標準で提供されています。

Table.2 (b)のC言語のプログラムでは、このconv関数に相当する関数がないため、③に示されるように伝達関数を掛け合わせる関数を作成する必要があります。④と⑤の部分は、それぞれMATLAB^®のプログラムの①、②に対応する処理を行っています。また、確認のために伝達関数の係数の計算結果をTable.2 (c)に示します。

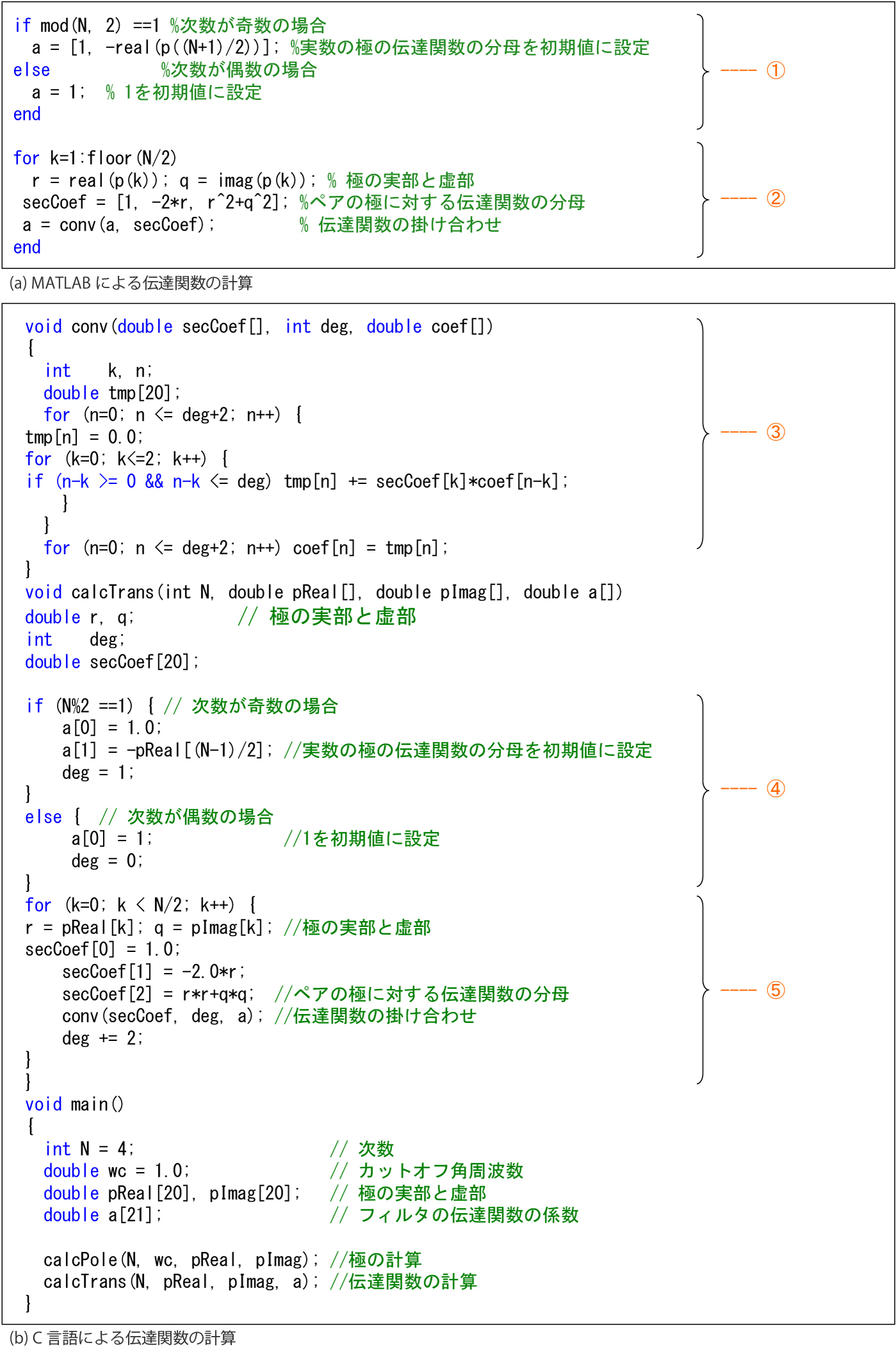Table.2　フィルタの伝達関数の計算